2.1 不等式的基本性质

2.1.1 实数的大小

实数与数轴上的点之间可以建立一一对应的关系。

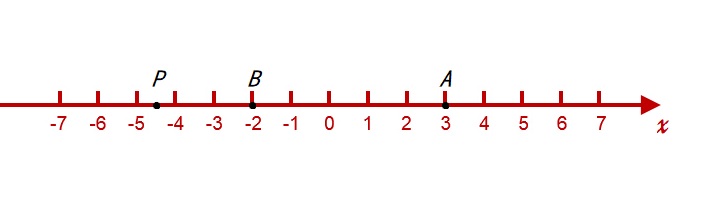
在上图中，点 $A$ 与数 $3$ 对应，点 $B$ 与数 $-2$ 对应等。

可以看到当数轴上一动点 $P$ 从左向右移动时，它对应的实数就从小到大变化。

这就是说，数轴上的任意两点中，右边的点对应的实数比左边的点对应的实数大。

例如，点 $A$ 位于点 $B$ 的右边，则点 $A$ 对应的实数 $3$ 比点 $B$ 对应的实数 $-2$ 大，即 $3 < -2$。

同样有 $3 > -3$、$0 > -2$、$3 > 0$、$-3 > -4$、$4 > 3$ 等。

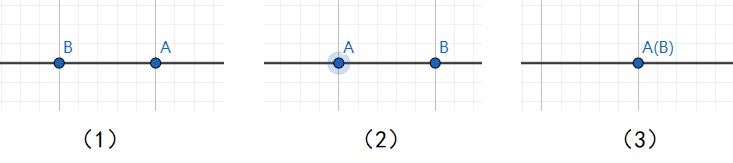
在上图中，设 $A$、$B$ 为任意两个实数，则 $A$、$B$ 在数轴上的位置有且只有以下三种：

（1）点 $A$ 在点 $B$ 右侧（上图(1)）；（2）点 $A$ 与点 $B$ 重合（上图(2)）；（3）点 $A$ 与点 $B$ 左侧（上图(3)）；

相应的，实数 $A$、$B$ 的关系为：

（1）$\Huge A > B$ （2）$\Huge A = B$ （3）$\Huge A < B$

上面三个式子的另一表达方法是：

1. $\Huge A - B > 0 \hArr A > B$
2. $\Huge A - B = 0 \hArr A = B$
3. $\Huge A - B < 0 \hArr A < B$

含有不等号（$<, =, >, \le, \ge, \not =$）的式子，叫做 不等式。

2.1.2 不等式的基本性质

从实数大小的基本性质出发，可以证明下列不等式的重要性质。

传递性 通常叫做 不等式的传递性。

加法法则 与 乘法法则 通常叫做 作差比较法。

传递性

性质

如果 $a > b, b > c$ 则 $a > c$。

分析

要证 $a > c$，只要证 $a - c > 0$。

证明

因为 $a - c = (a - b) + (b - c)$
又由 $a > b, b > c$ ，即 $a - b > 0, b - c > 0$
所以 $(a - b) + (b - c) > 0$
因此 $a - c > 0$
即 $a > c$

加法法则

不等式的两边同时加上（或同时减去）同一个实数，不等号的方向不变。

性质

如果 $a > b$ ，则 $a + c > b + c$。

证明

因为 $(a + c) - (b + c) = a - b$
又由 $a > b$ ，即 $a - b > 0$
所以 $a + c > b + c$

乘法法则

如果不等式两边都乘同一个正数，则不等号方向不变，如果都乘同一个负数，则不等号的方向改变。

性质

如果 $a > b, c > 0$ 则 $ac > bc$；如果 $a > b,c < 0$ 则 $ac < bc$。

证明

因为 $ac - bc = (a - b)c$
又由 $a > b$ ，即 $a - b > 0$
所以：

• 当 $c > 0$ 时，$(a - b)c > 0$ ，即 $ac > bc$；
• 当 $c < 0$ 时，$(a - b)c < 0$ ，即 $ac < bc$；

推论：如果 $a + b > c$ ，则 $a > c - b$

不等式中任何一项，变号后可以从一边移到另一边。

证明

因为 $a + b > c$
所以 $a + b + (-b) > c + (-b)$ （加法法则）
即 $a > c - b$

推论：如果 $a > b$ ，且 $c > d$ ，则 $a + c > b + d$

两个或几个同向不等式，两边分别相加，所得的不等式与原不等式同方向。

证明

因为 $a > b$
所以 $a + c > b + c$ （加法法则）
因为 $c > d$
所以 $b + c > b + d$
因此 $a + c > b + d$ （传递性）

推论：如果 $a > b > 0$ ，且 $ c > d > 0$ ，则 $ac > bd$

两个或几个两边都是正数的同向不等式，把它们的两边分别相乘，所得的不等式与原不等式同向。

证明

因为 $a > b$ ，且 $b > 0$
所以 $ac > bc$ （乘法法则）
因为 $c > d$ ，且 $b > 0$
所以 $bc > bd$
因此 $ac > bd$ （传递性）