1.1 集合及其运算

1.1.1 集合的概念

参考： 集合概念_百度百科

集合概念关键字

对象：可以感觉到的客观存在以及思想中的事物或抽象符号，都可以称作对象。

集合：把一些能够确定的不同的对象看成一个整体，就说这个整体是由这些对象的全体构成的集合。

元素：集合中每个对象叫做这个集合的元素。

集合有时也简称为 集。 含有有限个元素的集合叫做 有限集，含有无限个元素的集合叫做 无限集。

集合中元素的特性

1. 确定性：作为集合的元素，必须是能够确定的。
2. 互异性：集合中的元素一定是不同的。
3. 无序性：集合中的元素没有固定的顺序。

集合符号

$\Large \in$ ：属于；

$\Large \notin$ ：不属于；

$\Large \mathbf{N}$ ：由全体非负整数构成的集合，叫做 自然数集 或 非负正数集；

$\Large \mathbf{N_+}$ 或 $\Large \mathbf{N^*}$ ：非负整数集 内排除 0 的集合，叫做 正整数集；

$\Large \mathbf{Z}$ ：由全体整数构成的集合，叫做 整数集；

$\Large \mathbf{Q}$ ：由全体 有理数 构成的集合，叫做 有理数集 ；

$\Large \mathbf{R}$ ：由全体 实数 构成的集合，叫做 实数集 ；

1.1.2 集合的表示方法

列举法

当集合元素不多时，可以直接将元素列举出来，并写在花括号（ $\{\}$ ）内，这种表示集合的方法叫做 列举法：

$$\Huge \{1, 2, 3, 4, 5, 6\}$$

性质描述法

$$\Huge A = \{x∈I | p(x)\}$$

在上式中，竖线（ $|$ ）左边表示集合 $A$ 中的任意一个元素，并标出元素的取值范围， 竖线（ $|$ ）右边表示只有集合 $A$ 内的元素才具有的 特征性质 。

在某种约定下，$x$ 的取值合集可省略不写，例如上式可简写为 $\Large A = {x | p(x)}$ 。

1.1.3 集合之间的关系

集合关系符号

$\Large \subseteq$ ：包含于；

$\Large \supseteq$ ：包含；

$\Large \varnothing$ ：空集；

$\Large \subsetneqq$ ：真包含于；

$\Large \supsetneqq$ ：真包含；

子集

如果集合 $A$ 的任意一个元素都是集合 $B$ 的元素，那么集合 $A$ 叫做集合 $B$ 的 子集，记作：

$$\Huge A \subseteq B 或 A \supseteq B$$

读作“$A$ 包含于 $B$” 或 “$B$ 包含 $A$”。

空集

不含任何元素的集合叫做 空集，记作 $\Large \varnothing$。

空集 是任意一集合的子集。

真子集

如果集合 $A$ 是集合 $B$ 的子集，并且 $B$ 中至少有一个元素不属于 $A$，那么集合 $A$ 叫做 集合 $B$ 的 真子集，记作：

$$\Huge A \subsetneqq B 或 B \supsetneqq A$$

读作“$A$ 真包含于 $B$”或“$B$ 真包含 $A$”。

真子集与子集的区别：

• 子集就是一个集合中的全部元素是另一个集合中的元素，有可能 与另一个集合相等；
• 真子集就是一个集合中的元素全部是另一个集合中的元素，但不存在 相等；

维恩图（Venn diagram）

参考 维恩图_百度百科

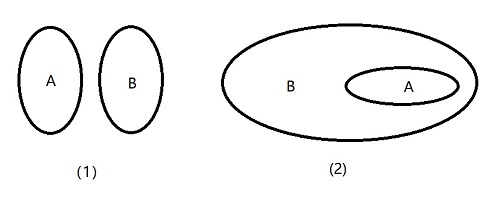
通常使用平面上一个封闭曲线的内部表示一个集合，如上图（1）。

如果集合 $A$ 是集合 $B$ 的 真子集，那么把表示 $A$ 的区域画在表示 $B$ 的区域内部，如上图（2）。

集合相等

如果两个集合的 元素 完全相同，那么就可以说这两个 集合相等。

集合 $A$ 等于集合 $B$，记作：

$$\Huge A = B$$

由相等的定义，可得：

如果 $A \subseteq B$ 且 $B \subseteq A$，那么 $A = B$； 反之，如果 $A = B$，那么 $A \subseteq B$ 且 $B \subseteq A$；

1.1.4 集合的运算

交集

给定两个集合 $A$、$B$，由既属于 $A$ 又属于 $B$ 的所有公共元素所构成的集合，叫做 $A$、$B$ 的 交集，记作：

$$\Huge A \cap B$$

读作“$A$ 交 $B$”

并集

给定两个集合 $A$、$B$，把它们所有的元素合并在一起构成的集合，叫做 $A$ 与 $B$ 的 并集，记作：

$$\Huge A \cup B$$

读作“$A$ 并 $B$”

全集与补集

在研究集合与集合之间的关系时，如果一些集合都是某一给定集合的子集，那么称这个给定的集合为这些集合的 全集，通常用 $U$ 表示。

如果 $A$ 是全集 $U$ 的一个 子集，由 $U$ 中的所有不属于 $A$ 的元素构成的集合，叫做 $A$ 在 $U$ 中的 补集，记作：

$$\Huge \complement _ U A$$

读作“$A$ 在 $B$ 中的补集”。