3.1 函数

3.1.1 函数的概念

变量与常量

变量（variable）：没有固定的值，可以改变的量；

常量（constant）：保持不变的量；

自变量与因变量

自变量（Independent variable）： 能够影响其他变量的变量叫做 自变量。

因变量（dependent variable）： 随着 自变量 的变化而变化，且 自变量 取唯一值时，因变量（函数）有且只有唯一值与其相对应。

函数三要素

函数 的三要素是：

1. 定义域（domain of definition）、
2. 值域（range）、
3. 对应法则（corresponding rule）。

$$\Huge y=f(x)$$

在上式中 $x$ 为 自变量，$y$ 为 因变量。 自变量 $x$ 的取值集合叫做函数的 定义域， 对应的 因变量 值 $y$ 的集合叫做函数的 值域。

在上式中对 $x$ 取值为 $a$，$y$ 的值也随之被确定为 $b$，$b$ 就叫做 $a$ 的 函数值。

在上式中表示 变量 $y$ 是 变量 $x$ 的 函数， 其中字母 $f$ 就抽象地表示 变量 $y$ 与 变量 $x$ 的 对应法则。

3.1.2 函数的表示方法

函数 概念的核心是 变量 $y$ 与 变量 $x$ 之间的 对应法则。 表示 对应法则 的方法是多种多样的，通常有：

解析法（分析法、公式法）

$$\Huge s=100t \quad (0 \le t \le 2)$$

在上式中给出了 自变量 $t$ 与 应变量 $s$ 的关系，这种表示函数的方法叫做 解析法（analytic method） ， 并且这个等式叫做 函数 的 解析式。

也叫：分析法 或 公式法。

列表法

把 函数 的 自变量 与 因变量 的值列成表格来表示函数，这种方法叫 列表法。

图像法

用“图形”来表示 函数的图像 ， 这种方法叫做 图像法。

3.1.3 函数的单调性

函数的 单调性（monotonicity） 也叫函数的增减性，可以定性描述在一个指定区间内，函数值 变化与 自变量 变化的关系。

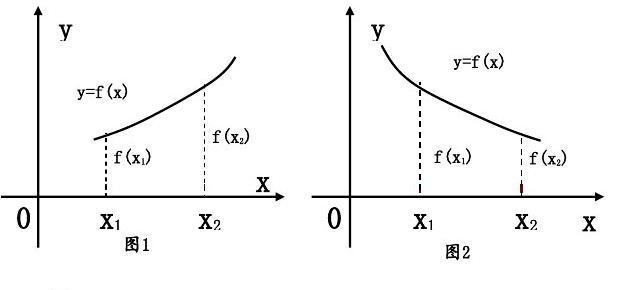
增函数与减函数

如上图 1，函数 $f(x)$ 的 自变量 在其定义区间内增大（或减小）时，函数值 也随着增大（或减小），这时称函数在这个区间上是 增函数。

如上图 2，函数 $f(x)$ 的 自变量 在其定义区间内增大（或减小）时，函数值 反而随着减小（或增大） ，这时称函数在这个区间上是 减函数。

由函数解析式判断函数是增函数还是减函数

已知函数 $y = f(x)$ ，在给定区间上，它的图象由上图所示，在此图象上任意取两点 $A(x_1, y_1), B(x_2, y_2)$ ，记作：

$$\Large \begin{align*} \Delta x &= x_2 - x_1 \\ \Delta y &= f(x_2) - f(x_1) \\ &= y_2 - y_1 \end{align*}$$

$\Delta x$ 表示自变量 $x$ 的增量，$\Delta y$ 表示自变量 $y$ 的增量。

这时，对于属于这个区间的任意两个不相等是值 $x_1, x_2$ ：

• 这个函数是增函数的充要条件是 $\large \frac{ \Delta y }{ \Delta x } > 0$ ；
• 这个函数是减函数的充要条件是 $\large \frac{ \Delta y }{ \Delta x } < 0$ ；

由此得到，由一个函数的解析式判断一个函数是增函数还是减函数的步骤：

1. 计算 $\large \Delta x$ 和 $\large \Delta y$
2. 计算 $\large k = \frac{ \Delta y }{ \Delta x }$
   • 当 $k > 0$ 时，函数 $y = f(x)$ 在这个区间上是增函数（上图 (1)）;
   • 当 $k < 0$ 时，函数 $y = f(x)$ 在这个区间上是增函数（上图 (2)）;

如果一个函数在某个区间上是增函数或减函数，就说这个函数在这个区间上具有（严格的）单调性。

3.1.4 函数的奇偶性

奇函数

若对函数 $f(x)$ 定义域内的任意一个 $x$ 值，都有 $\large f(-x)=-f(x)$，则称之为 奇函数。

一个函数是奇函数的充要条件是，它的图象是以坐标原点为对称中心的中心对称图形。

偶函数

若对函数 $f(x)$ 定义域内的任意一个 $x$ 值，都有 $\large f(-x)=f(x)$，则称之为 偶函数。

一个函数是偶函数的充要条件是，它的图象是以 $y$ 轴为对称轴的轴对称图形。

判断函数的奇偶性

在奇函数和偶函数的定义中，都要求函数的定义域对应的区间关于坐标原点对称， 如果一个函数的定义域对应的区间关于坐标原点不对称，这就失去了函数是奇函数或是偶函数的前提条件， 函数也就无奇偶性可言。

判断一个函数 $\large y = f(x) (x \in A)$ 的奇偶性步骤如下：

1. 判断定义域是否关于原点对称，即当 $x \in A$ 时，是否有 $-x \in A$
2. 当 1 成立时，对于任意一个 $x \in A$
   • 若 $\large f(-x) = -f(x)$ 则函数 $y = f(x)$ 是奇函数；
   • 若 $\large f(-x) = f(x)$ 则函数 $y = f(x)$ 是偶函数；